半圆弯拉下岩石内裂纹扩展有何规律

半圆弯拉下岩石内裂纹扩展规律数值模拟研究

摘要:

岩石内部固有缺陷的存在和扩展是导致其断裂的重要因素，半圆弯拉试验是该领域的重要实验。为研究半圆弯拉下含三维内裂纹试件扩展路径及断裂特性，基于Franc3D有限元自适应网格划分技术开展含三维内裂纹SCB试样数值模拟，结果表明:(1)基于Franc3D软件的三维裂纹扩展与室内试验具有较好的一致性，该软件是三维裂纹数值模拟的重要工具。(2)通过M积分得到裂纹尖端应力强度因子，分析得出对称加载模型为KⅠ与底部加载跨距呈正相关的Ⅰ型断裂模式;非对称加载模型中出现复合断裂模式，随着右侧加载跨距的增加，KⅠ先降低再升高，KⅡ及KⅢ先变化至0，再逐渐升高。(3)基于最大拉应力准则得到裂纹扩展路径，对称加载模型在I型断裂模式下进行平面扩展后破坏，非对称加载模型出现复合断裂模式，伴随翼型起裂并扩展至破坏。(4)定量分析对称加载模型裂纹内部扩展规律得出，裂纹下端扩展速率最大，上端扩展速率最小。

关键词:

岩石断裂;半圆弯拉;Franc3D;扩展路径;三维裂纹;

张志韬(1994—),男,硕士研究生,主要从事断裂力学理论及试验相关的科研工作。E-mail:zhangzh@;

王海军(1985—),男,高级工程师,硕士研究生导师,博士,主要从事断裂力学理论及试验相关的科研工作。E-mail:hjwang@;

基金：

国家自然科学基金(51409170,51739008);

江苏省自然科学基金(BK20171130);

中央级公益性科研院研业务费项目(Y419005);

引用：

张志韬，顾浩，王海军，等.半圆弯拉下岩石内裂纹扩展规律数值模拟研究［J］.水利水电技术，2020，51(4):193202.

ZHANGZhitao，GUHao，WANGHaijun，irclebing［J］.WaterResourcesandHydropowerEngineering，2020，51(4):193-202.

半圆形弯曲(SCB)试样因其简单的几何结构、制造工艺、试验操作,广泛应用于岩石等脆性材料的断裂行为。如FENG等利用SCB试验,研究了温度对砂岩I型断裂韧性及断裂特征的影响。WANG等利用SCB试样裂缝与水力裂缝的相互作进行了物理实验研究。JIANG等利用石膏类3D打印材料进行SCB试验,与岩石材料致的断裂路径。HUANG等用带缺口SCB试件探究了沥青混合料的抗折性能。赵毅鑫等采用半圆弯拉法展样抗拉及断裂性能的研究。ALIHA等通过控制试样形状及加载参数对不同类型的三点弯曲的PMMA板进行和理论研究,并利用SCB试件开展了沥青混合料的混合型断裂韧度特性指标研究。

在理论及数值研究方面,LIM等于1993年提出了切口SCB试件的应力强度因子的方法,为混合模式下断裂究提供手段。FAYED等采用有限元程序对带边缘裂纹SCB的I/Ⅱ型应力强度因子(SIF)进行了计算。ZHA用离散元模型对含底部切槽的半圆弯拉试样的动态断裂韧性进行了数值模拟;EFTEKHARI等利用扩展有限讨论了在混合加载下带切口SCB试样的扩展路径及断裂性能。刘华博借助PFC3D离散元软件构建了花岗岩型,对单轴压缩下三维裂纹的起裂、扩展、微裂纹生长曲线等过程进行数值分析。FU等利用FLAC3D对石状树脂内单一裂纹在单轴和双轴压缩作用下的渐进破坏过程进行了三维数值模拟。

在理论和数值分析方面,当前研究多局限于表面和穿透裂纹,但是岩石等材料的裂纹多以三维内裂纹形式存断裂破坏性能影响巨大。而对于三维内裂纹任意扩展路径的模拟,建模、理论分析、网格处理都十分复杂,导致裂纹扩展路径模拟一直是断裂力学的难点问题。

针对以上问题,本文将利用Franc3D软件,建立含竖向内裂纹对称加载模型和非对称加载模型,基于M积分给裂纹尖端Ⅰ、Ⅱ、Ⅲ型K的分布规律,对该试样模型的断裂模式、扩展路径、破坏形态、扩展速率进行数值模为三维内裂纹扩展路径模拟、断裂特性研究提供数值基础,为相应的工程实际问题提供参考。

1.1Franc3D

为计算工程结构在任意复杂的几何形状、载荷条件和裂纹形态下的三维裂纹扩展,美国FAC公司联合康奈开发了Franc3D软件,利用该软件,可以展开准静态模式下任意三维裂纹的数值模拟。该软件常规工作流程如对Franc3D详细功能不做详细赘述,详见文献

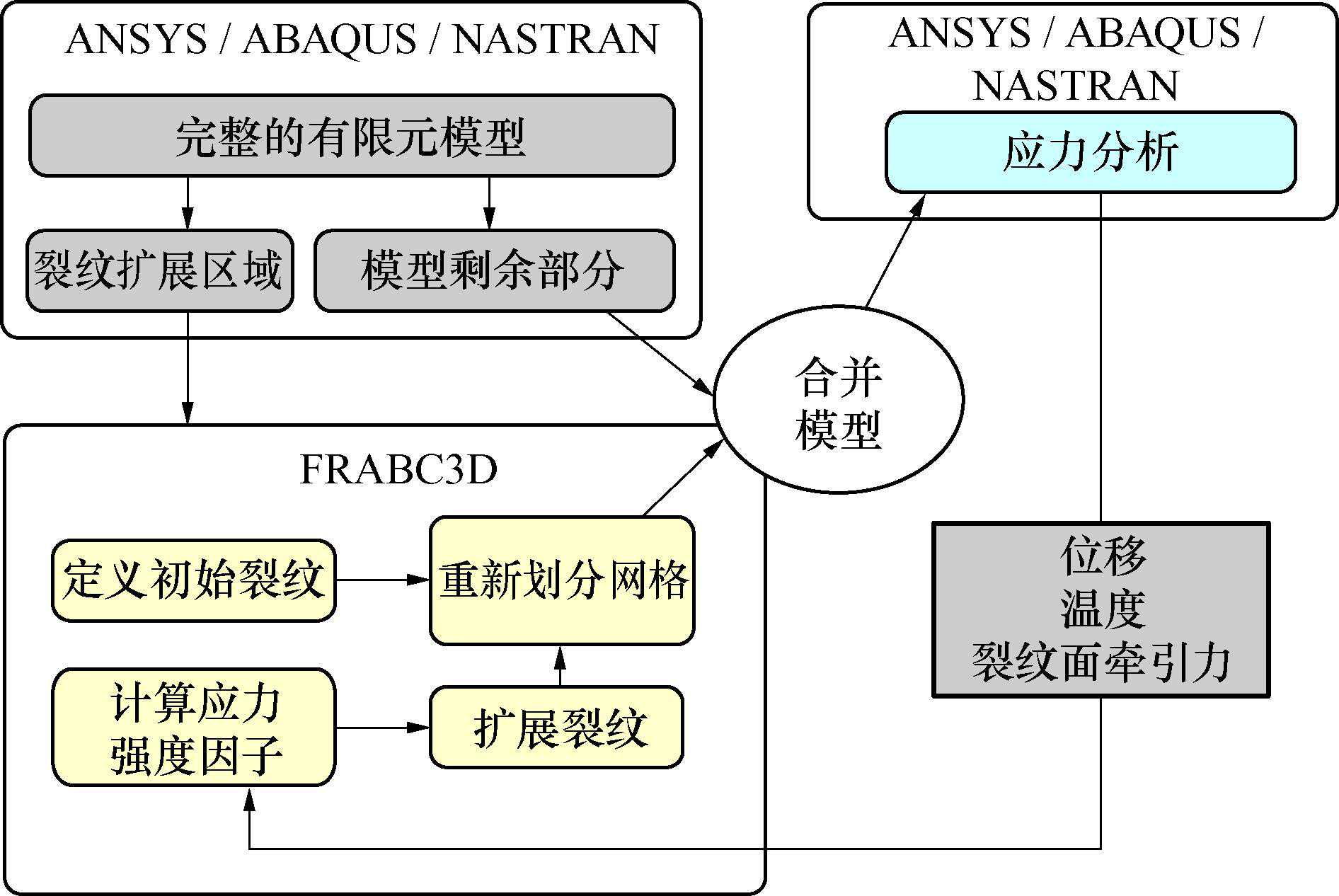
图1Franc3D工作流程

1.2数值模型及研究方案

1.2.1数值模型

本文建立两组含三维内裂纹模型如图2所示。试件为半圆状,半径R为50mm,厚度t为50mm。内裂纹形状特征尺寸a为10mm。内裂纹深度h为15.0mm。其中2S为底部加载跨距,S为左侧加载跨距,S为右侧加载跨

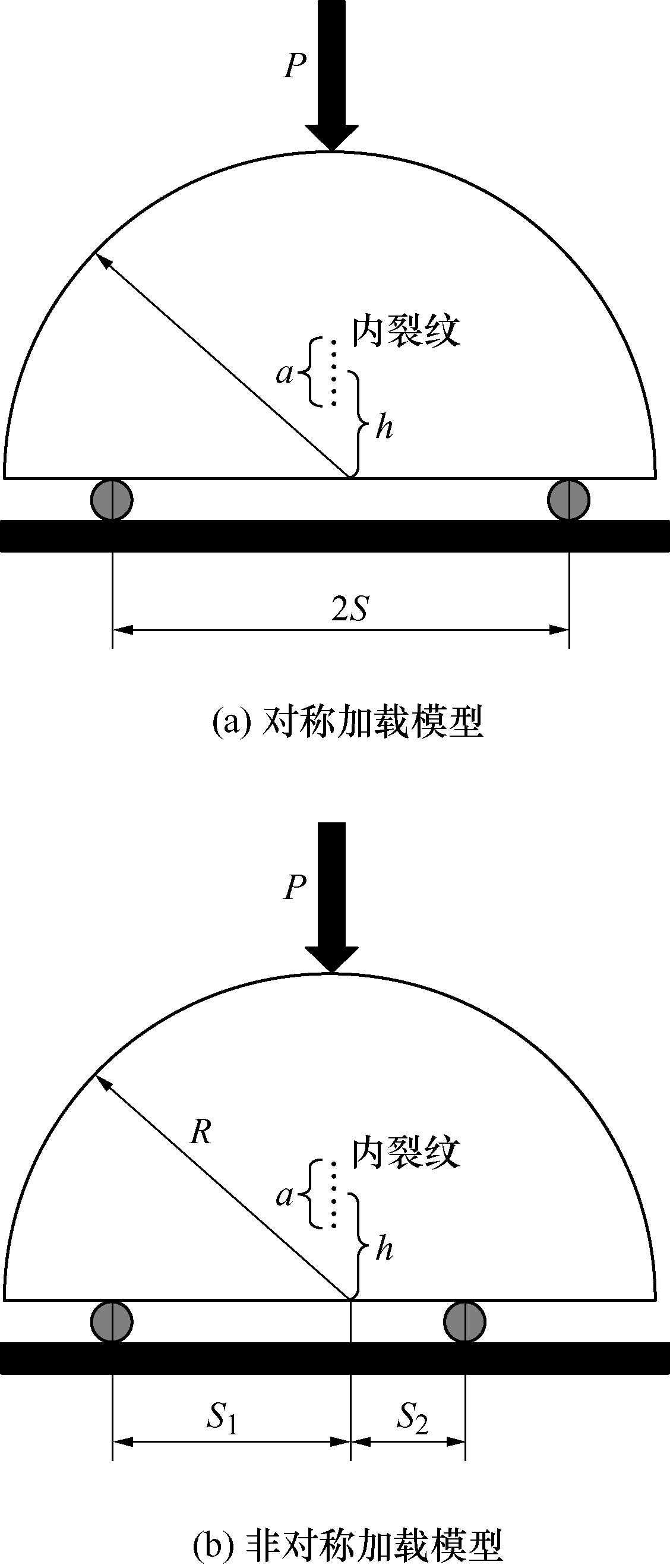
图2三维内裂纹模型试样设计示意

1.2.2研究方案

本次研究方案中,对称加载模型A组保持a/R、t/R不变,探究S/R的变化对三维内裂纹的扩展特征及断裂特响。非对称加载模型B组保持a/R、t/R、S/R不变,探究S/R的变化对三维内裂纹的扩展特征及断裂特性的影究方案如表1所列。需要说明的是,后文中为验证Franc3D模拟裂纹扩展路径的准确性建立的两种数值模型,仅考模型并未列入研究方案中。

图3给出了带预制内裂纹半圆弯拉试样的网格模型。有限元数值模拟中设置的相关参数列出如下:①材料为性弹性材料,弹性模量E=17.92GPa,泊松比ν=0.192,密度ρ=2.3g/cm;②模型上部施加y方向的应力边界;③模施加y方向固定的位移约束。

2数值模拟

2.1.1SIF计算原理

对于应力强度因子采用M积分的方法来计算,假设两个平衡状态叠加的交互J积分为

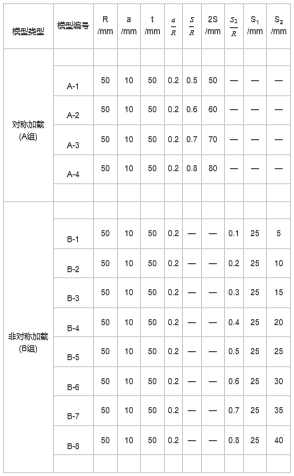
表1研究方案

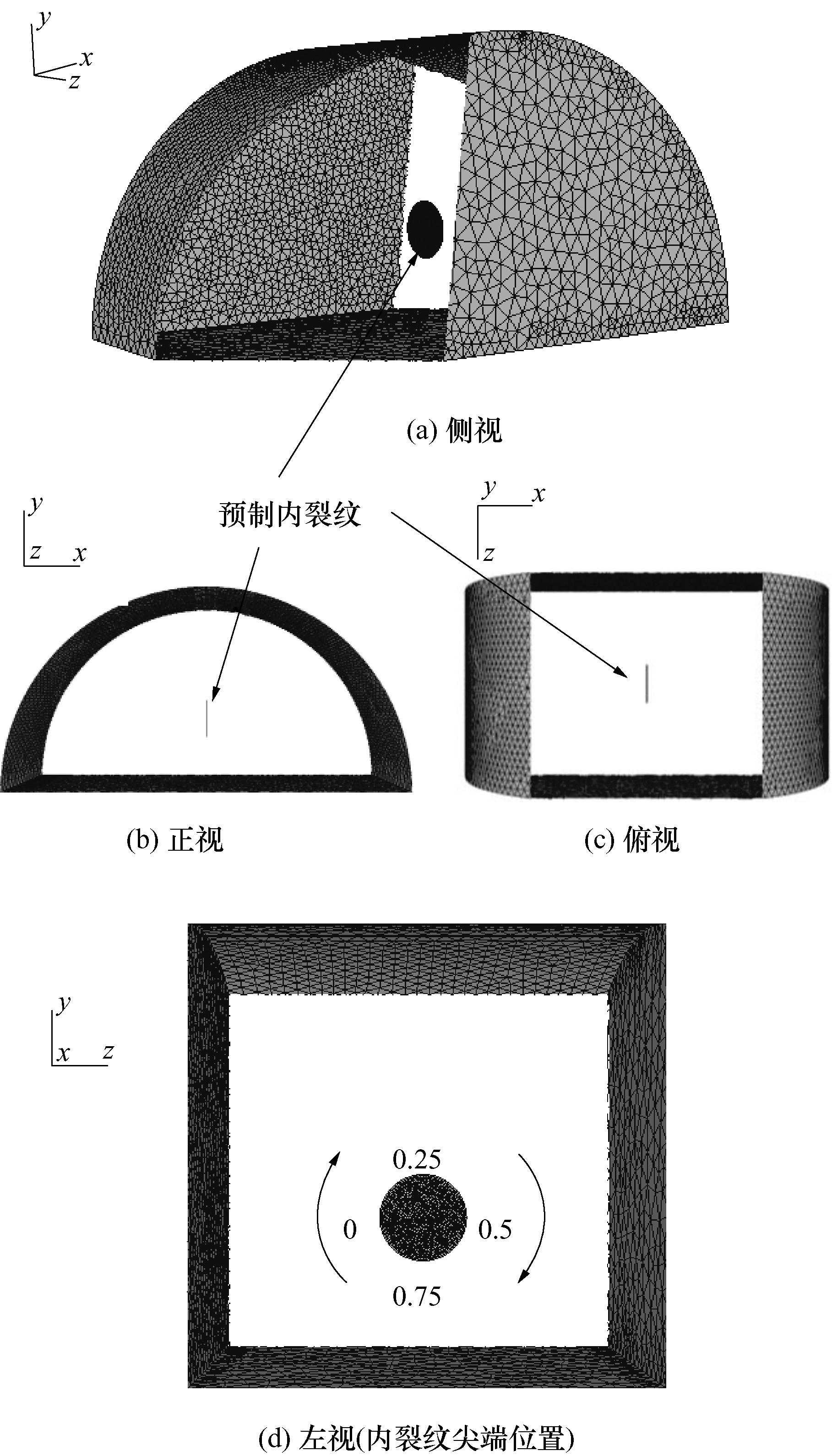
图3数值模型

通过选取特定辅助场,可由式(10),利用远场的交互M积分得到裂纹端部应力强度因子K、K和K的解。态1为问题的真实状态K=K,状态2由纯Ⅰ型裂纹的渐进解表示,且取

式中,Γ为远离裂尖的积分曲线;δ为克罗狄克符号;q为光滑函数;σ(1)ij、ε(1)ij、u(1)i均为有限元解;σ(2)ij、

(2)i分别为纯I、Ⅱ、Ⅲ型裂纹问题的裂尖渐近解。

由式(6)、式(13)、式(14)、式(15)可得到裂纹尖端的应力强度因子。

2.1.2T应力计算原理

T应力在Williams线性弹性裂纹尖端应力场的级数展开中,第二个非奇异项称为弹性T应力,表示平行于作用的应力。FRANC3D用的是T应力求解的一般办法,具体可参阅文献[21,22]的研究。

2.2室内试验验证

在进行数值模拟之前,首先开展Franc3D软件进行任意裂纹扩展路径模拟的准确性验证。为验证纯内裂纹径的合理性,首先对比文献[23],建立单轴拉伸下含水平内裂纹模型,数值模拟结果证明Franc3D在三维内裂纹扩的一致性。为验证本研究建模的正确性,基于ABAQUS初始模型,利用Franc3D分别对β=0°、β=30°、β=54°三切口角度的砂岩SCB试样进行建模,数值模拟结果与文献[4]具有较好的一致性。综上可知,在确保数值模型正提下,Franc3D可准确模拟三维内裂纹在三点弯拉下扩展断裂的全过程。数值模拟与室内试验结果如图4所示。

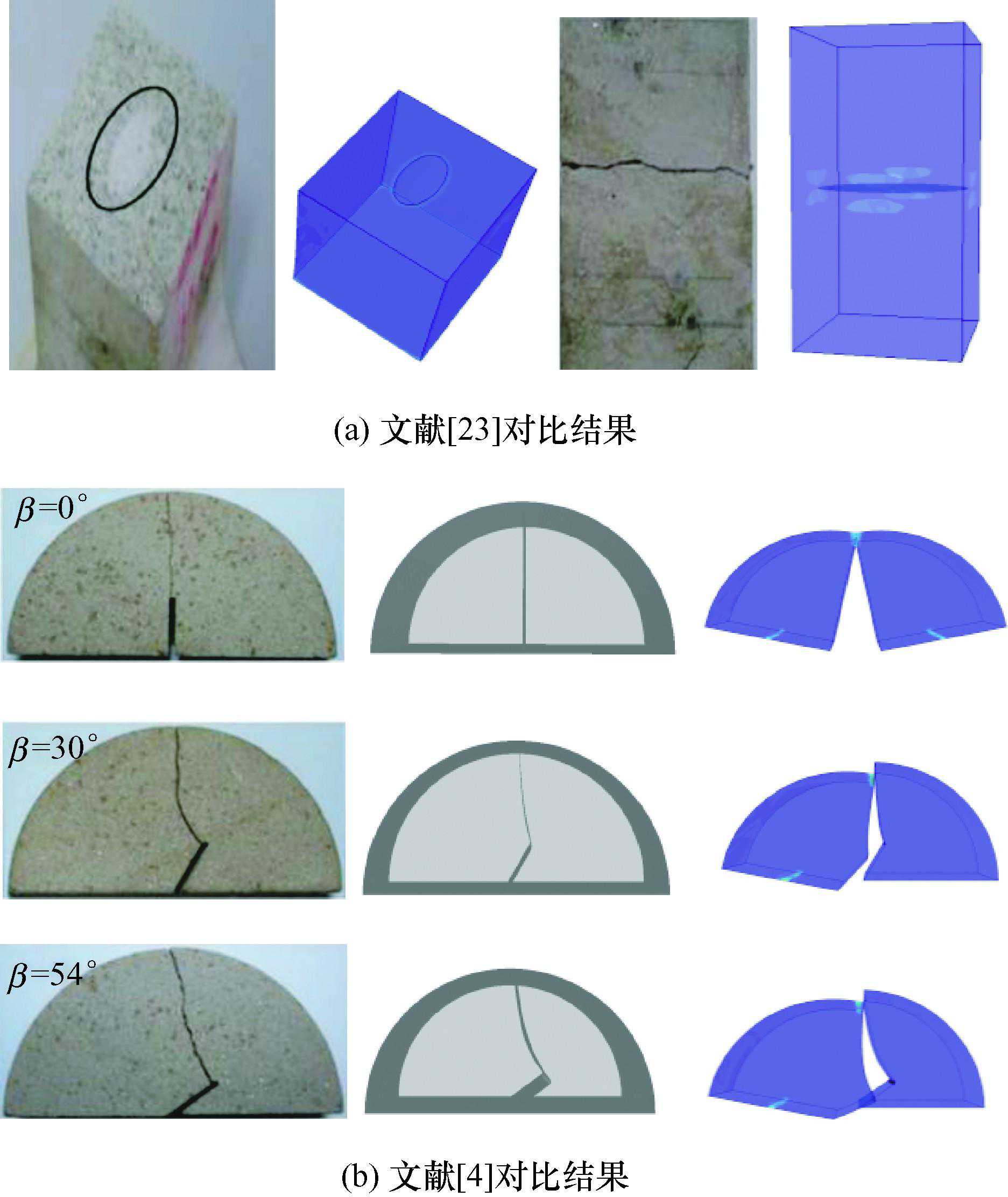
图4室内试验与数值模拟对比结果

利用M积分可同时计算出三种断裂模式的应力强度因子(K、K和K),应力强度因子描述了裂纹尖端附近异性的严重程度,而T应力也能显著影响裂纹的萌生和裂纹的扩展路径,Franc3D可以同时给出K、K、K的数值。

2.3.1对称加载模型

由本节应力强度因子分布可知,A组模型均为Ⅰ型断裂模式,此处仅以A-1模型的SIF分布加以分析论证。以裂纹尖端K为基准,定义K/│K│为归一化应力强度因子,其中n=Ⅰ、Ⅱ、Ⅲ。绘制A-1模型归一化应力子沿裂纹尖端一周的曲线如图5所示。

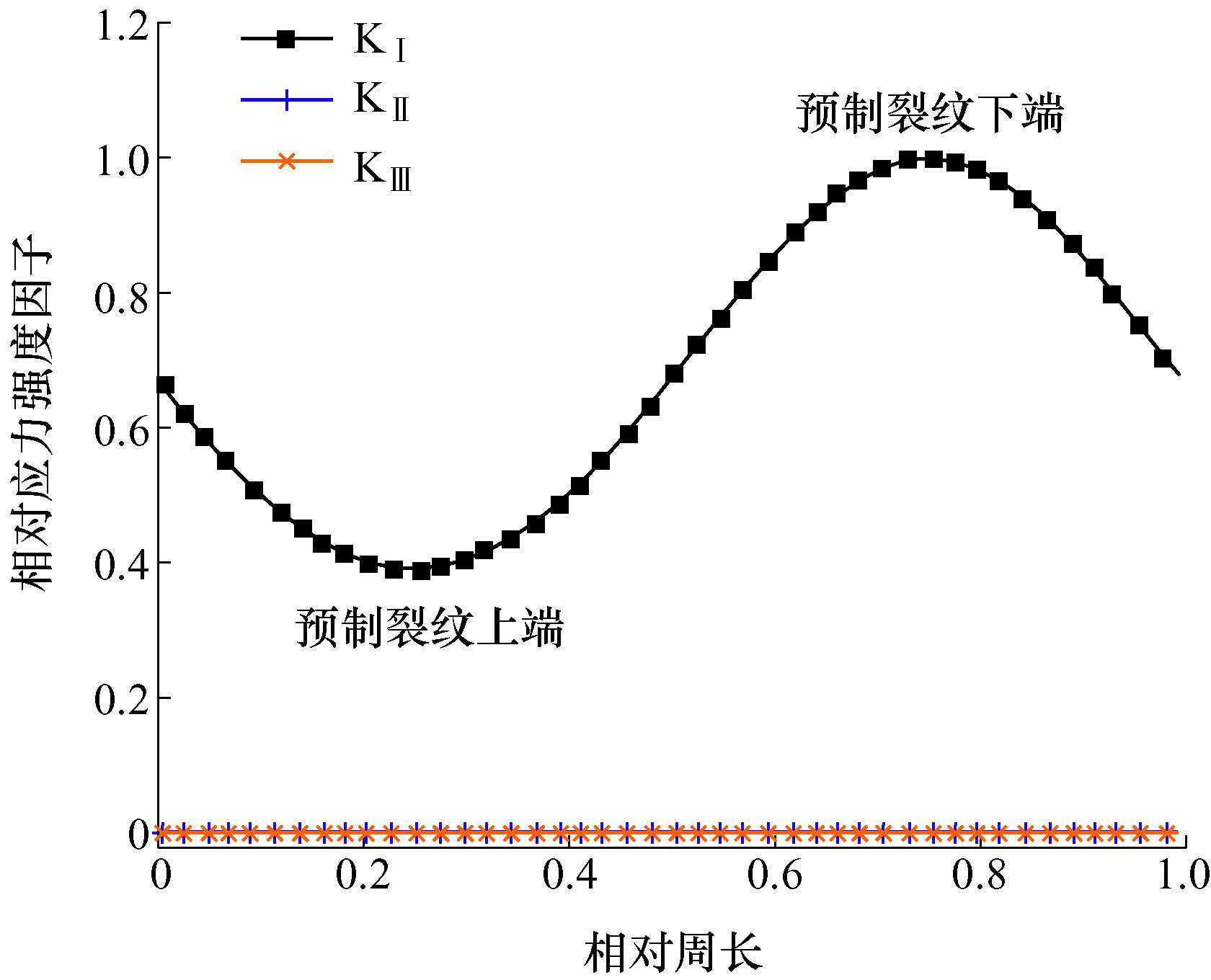
图5相对应力强度因子

分析应力强度因子,得到规律如下:

(1)相对于K的数量级,K、K的数值几乎可以忽略为零,这说明起裂前,裂纹面处于极大的张拉作用下,所更倾向于沿原裂纹面进行扩展,这与后文路径模拟中裂纹沿平面扩展相一致。

(2)裂纹下端K最大,上端K最小,这与后文数值模拟中裂纹下端扩展程度大,上端扩展程度小相一致。

为探究S/R的变化对Ⅰ型断裂模式下三维内裂纹的扩展特征及断裂特性的影响,绘制四组模型起裂前归一化力强度因子和T应力如图6和图7所示。

分析四组模型,得到规律如下:(1)由图6可知,固定a/R、t/R不变,裂纹前缘K随着S/R的增大而增大,此规律口SCB试样规律相同。(2)由图7可知,纯Ⅰ型断裂模式下,T应力恒为负值,这与文献[24,25]指出的在纯Ⅰ型式下,T应力为负时的裂纹扩展是稳定的,且扩展方向不发生偏转相一致。裂纹下端T应力随S/R的变化程度较裂更为剧烈。

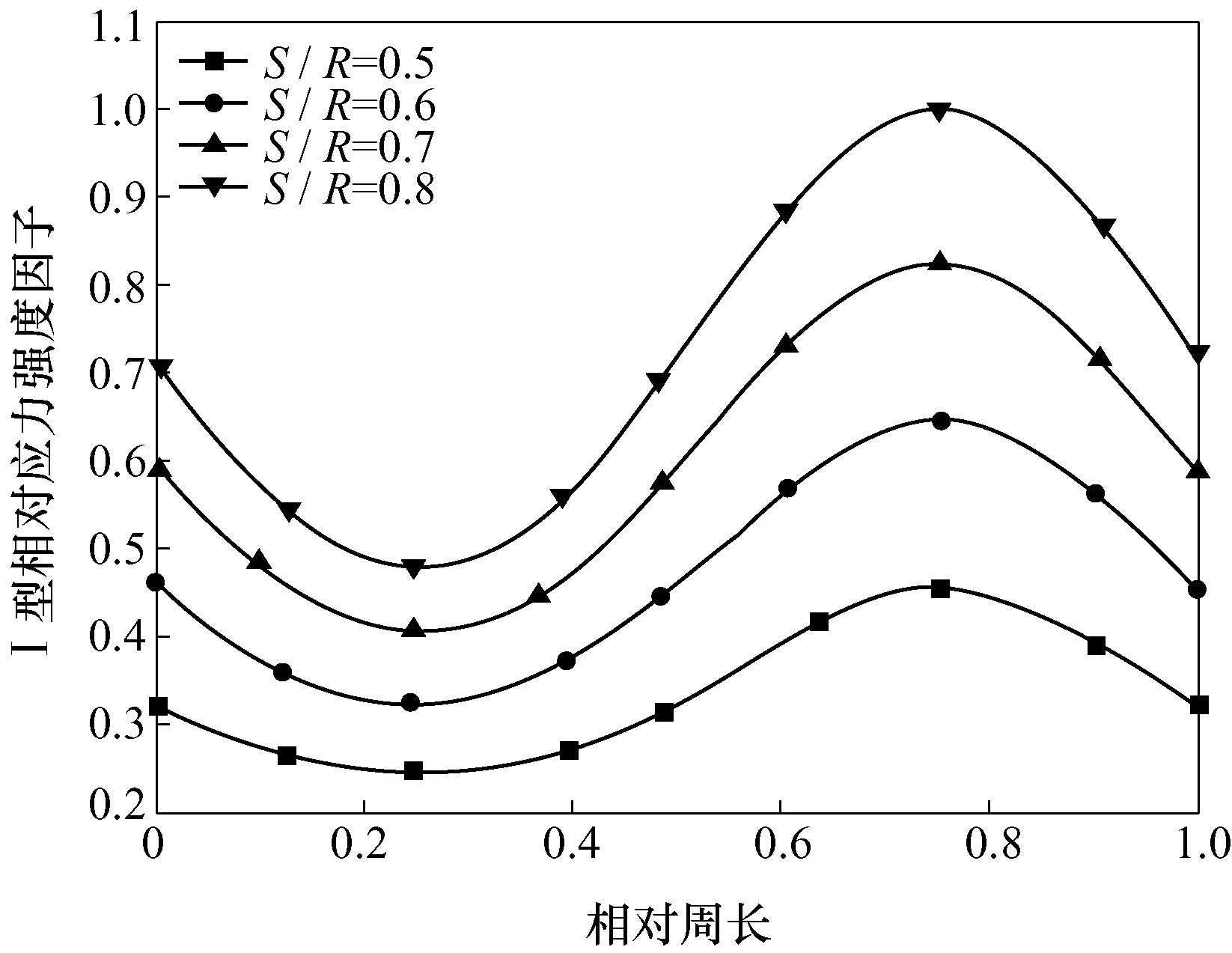
图6Ⅰ型相对应力强度因子

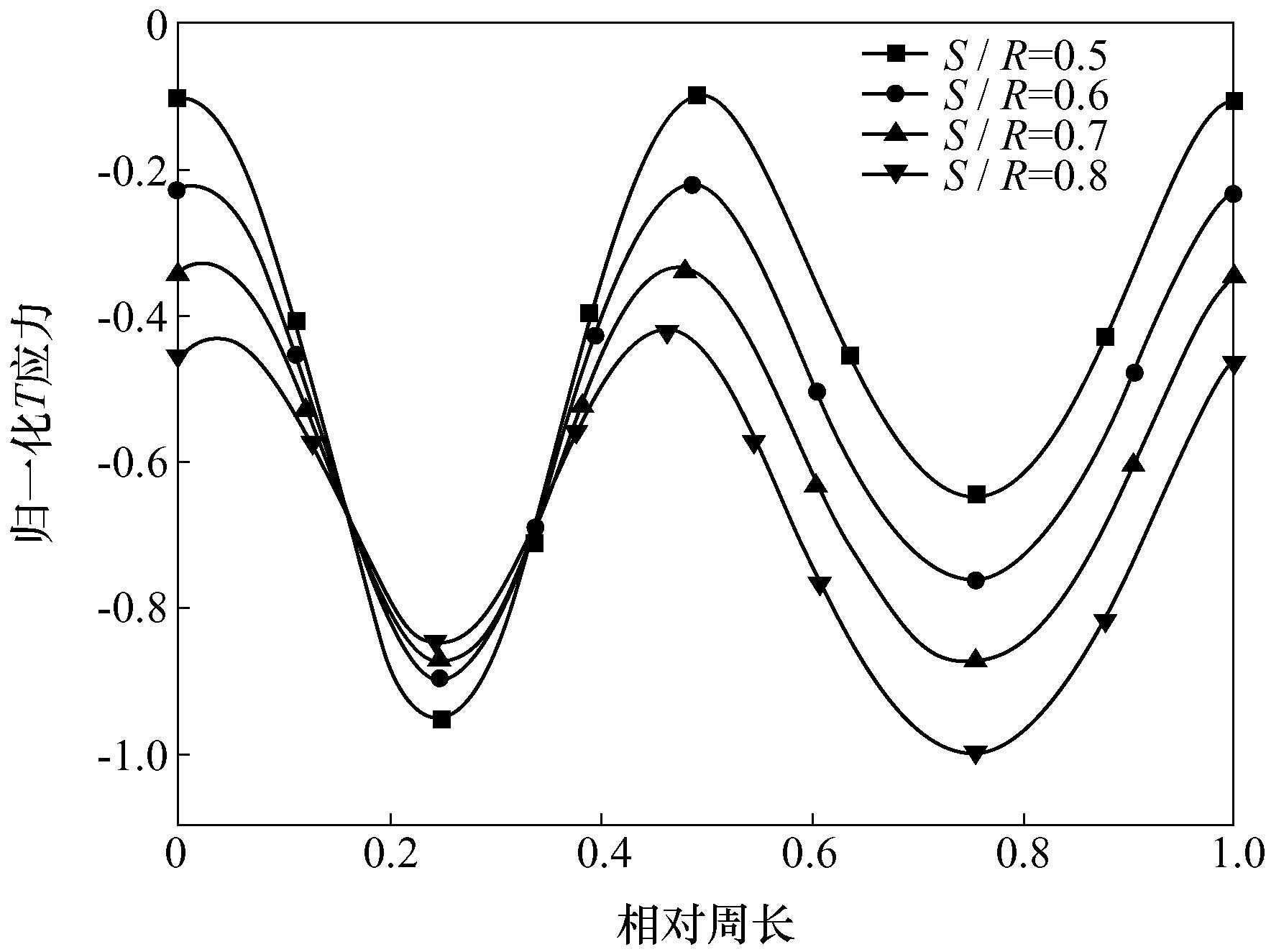
图7归一化T应力

2.3.2非对称加载模型

首先给出归一化应力强度因子变化规律如图8所示,分析如下:

(1)根据图8(a)—图8(c)的K、K、K分布规律可知B-4、B-5模型与对称加载模型K分布规律一致,判断Ⅰ型断裂模式,说明沿模型中心方向的小范围偏心作用对加载模式的影响较小。通过观察K分布并结合后文数值现的翼型裂纹形态,判断B-1、B-2、B-3、B-6、B-7、B-8模型为复合型断裂模式。

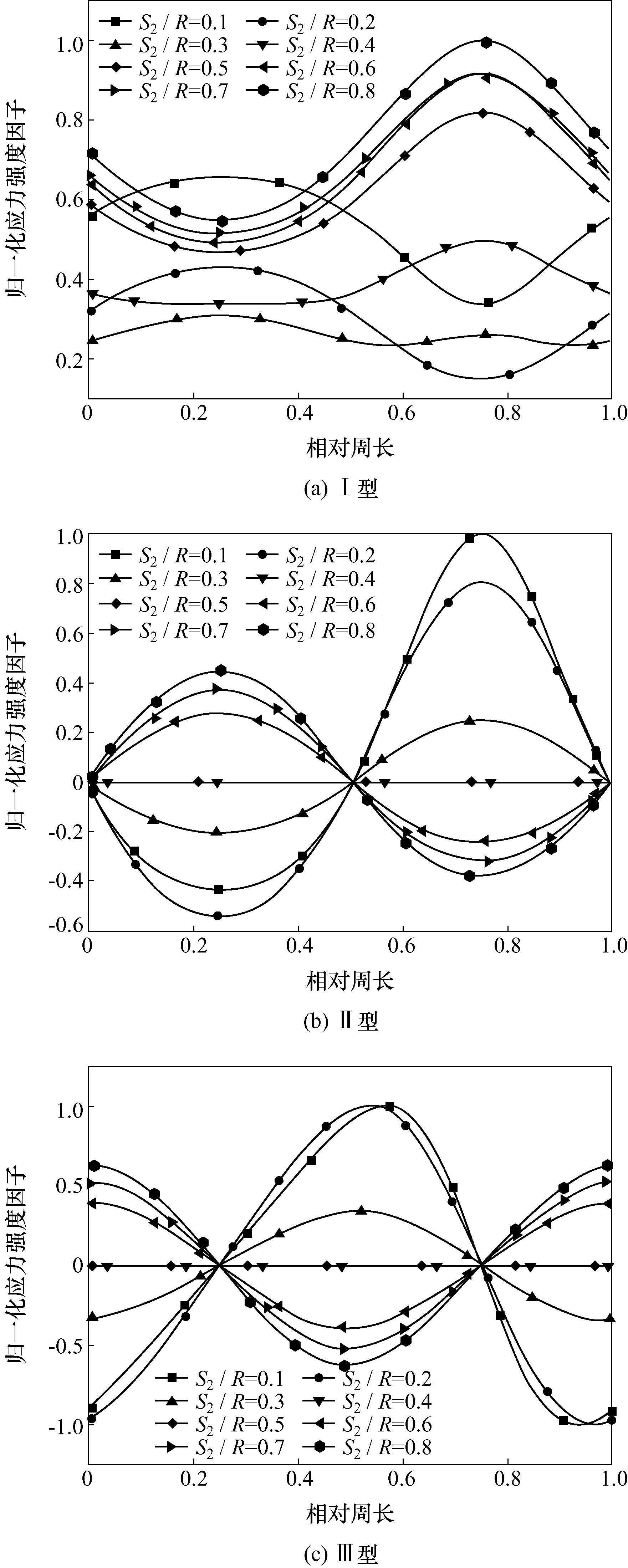
图8非对称加载模型相对应力强度因子

(2)分析图8(a)可知,随着S/R的增加,K先降低再升高。需要注意的是,从模型B-3可以看出,裂纹下端K的优先于上端,同时下端的I型作用升高程度更大。B-1、B-2、B-3模型的裂纹上端I型作用最强,下端最弱。余下模相反。

(3)通过图8(b)可以看出,随着S/R的增加,Ⅱ型作用先变化至0,再逐渐升高,且剪切作用方向发生改变。需要是,S/R数值较小时,Ⅱ型作用更强。B-1、B-2、B-3模型的裂纹下端Ⅱ型作用最强,B-6、B-7、B-8模型的裂纹型作用最强。

(4)通过图8(c)可知,与Ⅱ作用类似,随着S/R的增加,Ⅲ型作用先变化至0,再逐渐升高。该组所有模型中,Ⅲ裂纹尖端相对周长0、0.5、1.0附近处达到峰值。

(5)此处并未给出归一化T应力图像,需要说明的是目前的理论研究中对T应力的讨论多基于Ⅰ型或Ⅰ-Ⅱ型式下的二维问题,对纯三维内裂纹问题下的T应力的讨论分析并不常见,探讨T应力对纯三维内裂纹扩展机制的影后续数值研究中需要解决的问题之一。

2.4裂纹扩展准则及扩展机理

Franc3D提供了最大拉应力(mts)、最大剪应力(mss)、广义应力(gs)、能量释放率(serr)、平面扩准则。其中最大剪应力(mss)、广义应力(gs)和应变能释放率(serr)准则,可用于高剪切和材料允许剪切为主的展的情况。裂纹的局部扩展方向由“扭结”角决定(见图9)。而平面扩展准则将默认扭结角度为零,忽略了K的作

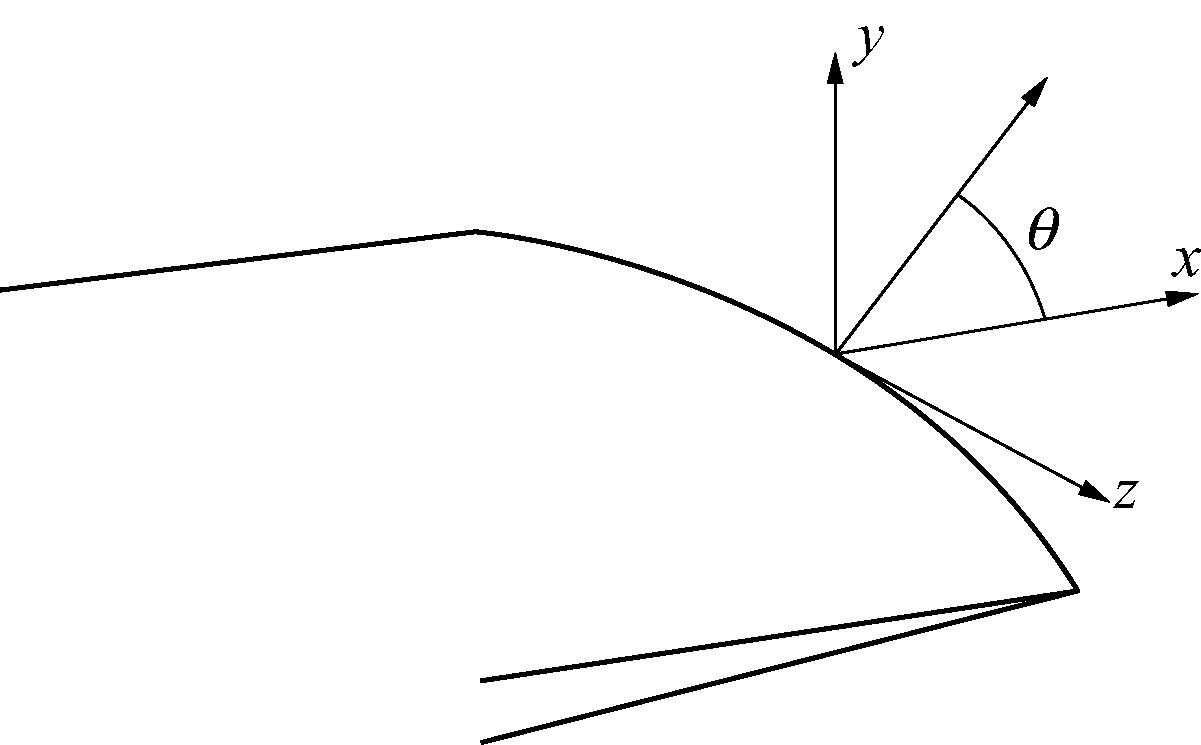
图9扭结角示意

本试样的数值模拟中,采用最大拉应力(mts)、准则,MTS理论预测裂纹将沿“环向”应力最大的方向扩展。针型具有的各向同性材料特性,环向应力与I型应力强度因子Kr相关,其中

ΚrΙ=σθθ√2πr(16)

准静态模型下,开裂方式由下式决定

∂σθθ(ΚⅠ,ΚⅡ,θ)∂θθ=0(17)

叠加张开型I和滑移型Ⅱ裂纹尖端附近应力场,并用极坐标形式表示如下

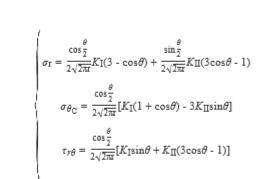
（18）

取开裂角为θ,将(18)代入式(17)可得

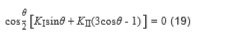
由cos

θ2=0,可解得θ=±π,此解在物理上不可能存在,因为裂纹不可能沿反方向扩展。

另一组解可由Ksinθ+K(3cosθ-1)=0求得。令λ=K/K,将该公式以θ角为未知数解出为

由于|θ|应小于π/2(否则裂纹将折向反方向扩展),为保证这一条件,式(20)只取负号,即

裂纹尖端应力场如图10所示。

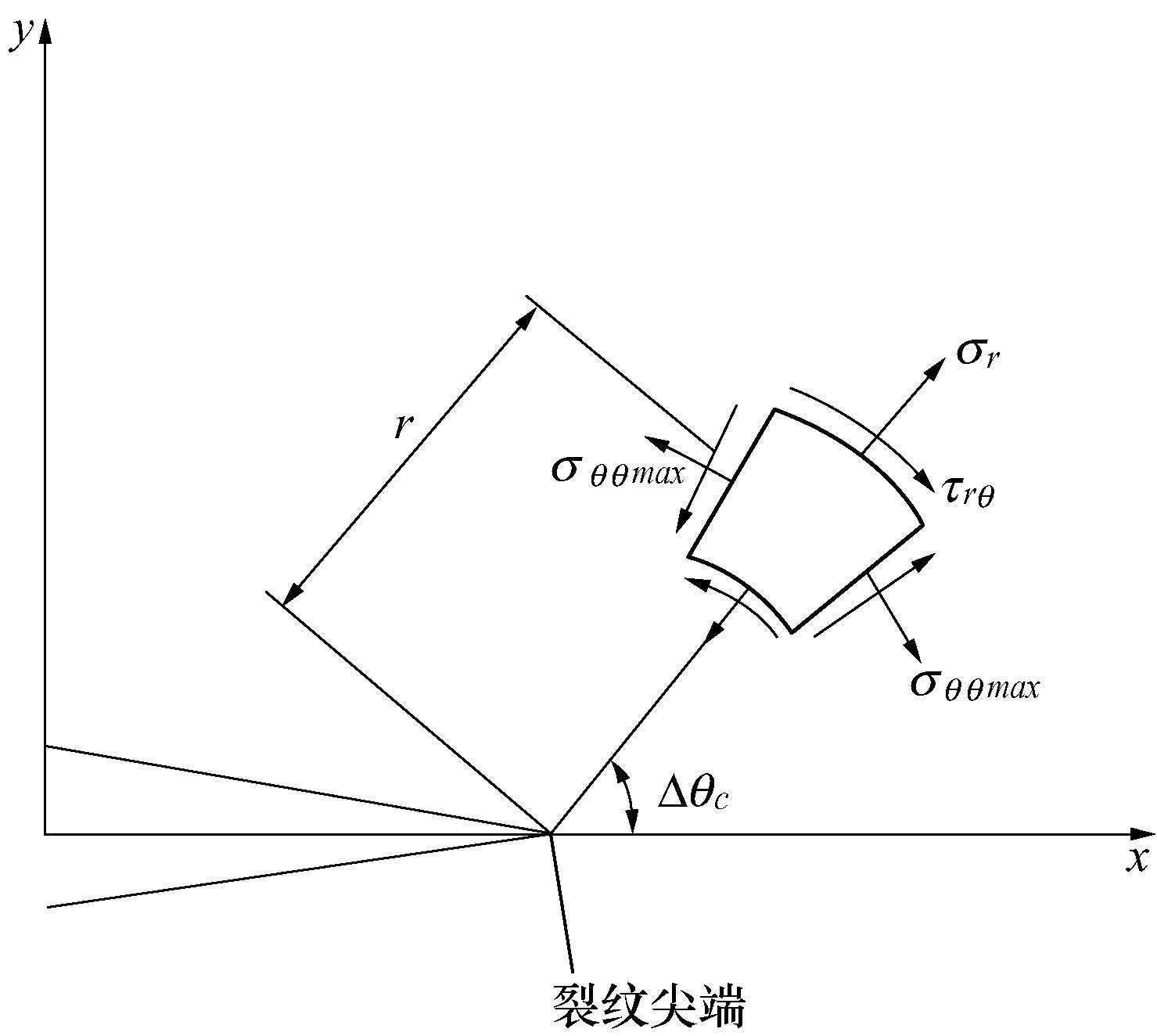
图10裂纹尖端应力场

M积分计算出的应力强度因子用于预测裂尖的扩展方向和扩展程度,此过程分三个步骤:(1)基于极坐标下的缘各个节点的应力状态计算其局部扭结角度;(2)使用准静态模型计算各个有限元节点局部裂纹扩展的相对量多项式曲线推断和平整裂纹面。裂纹前沿扩展机理如图11所示。

2.5裂纹扩展模拟结果

图12和图13给出了两组模型裂纹扩展与破坏路径(以模型A-1、B-8为例),便于读者更好的从整体上把握试过程。然后详细展开对裂纹扩展路径、破坏过程、裂纹扩展速率的分析。

通过观察两个模型内裂纹扩展路径及破坏过程,得到规律如下:

(1)A-1模型内裂纹在I型断裂模式下进行平面扩展,裂纹下端先到达试样底部,之后裂纹迅速向四周扩展,最后穿裂纹使试样断裂成对称的两部分。

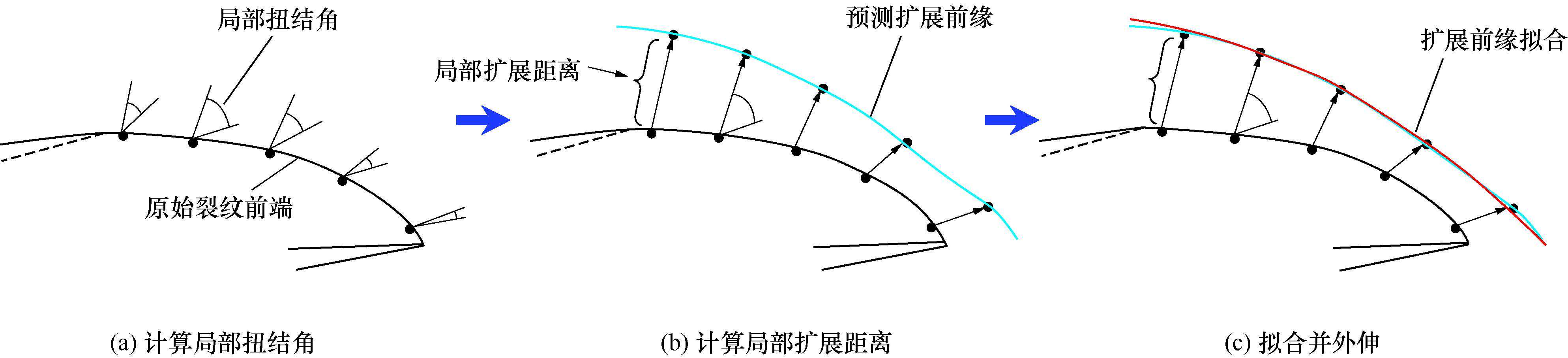
图11裂纹前沿扩展机理

图12模型裂纹扩展破坏过程

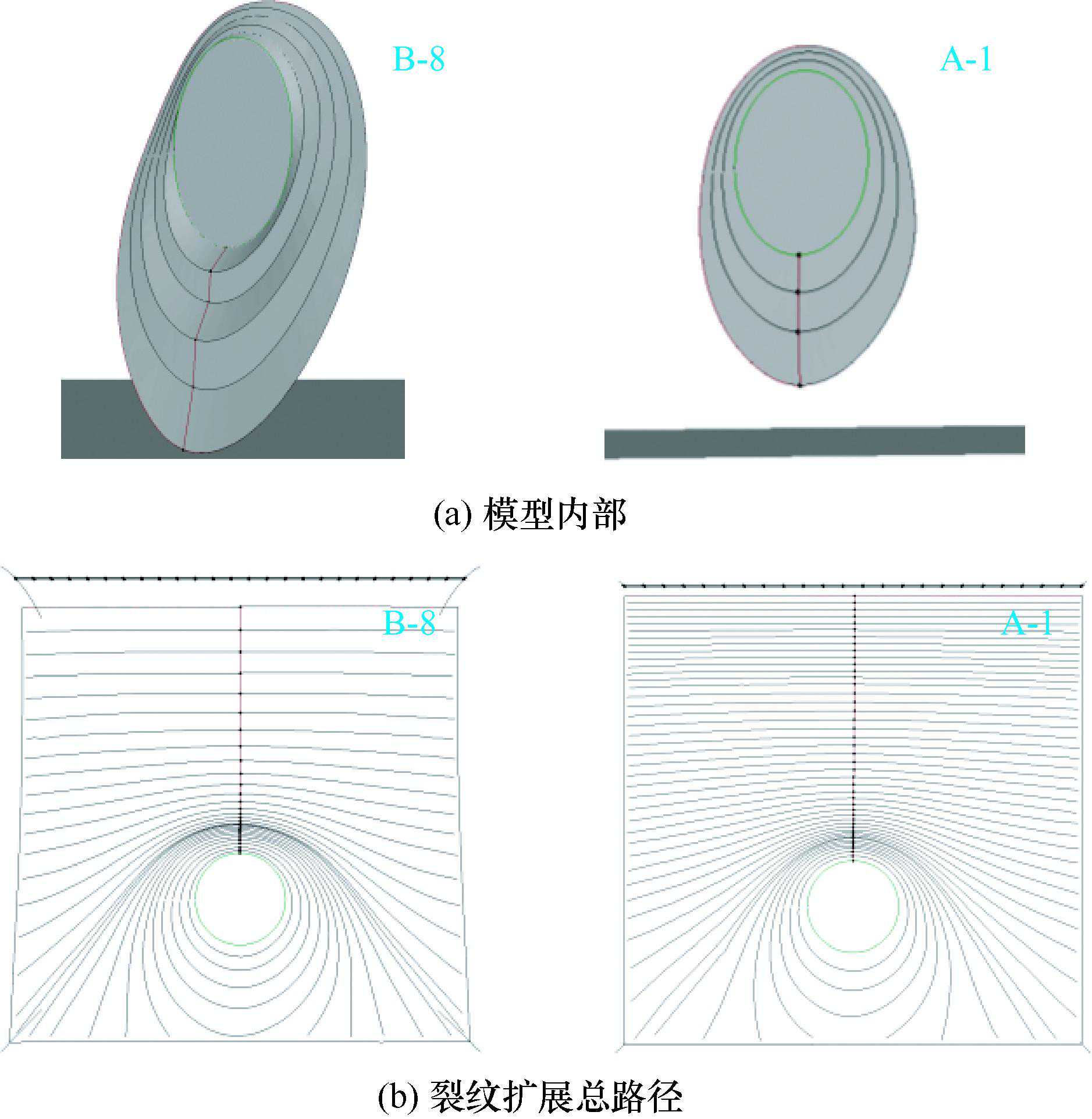
图13模型裂纹扩展破坏路径

2.6裂纹扩展速率

为定量分析A组对称加载模型裂纹起裂到即将扩展至式样底部的扩展规律,选取该阶段进行分析。为得到扩展步长默认为裂纹半径的15%～20%,裂尖单元环半径默认为裂纹半径的10%。本阶段设置扩展步长为裂纹5%,为0.75mm,保持不变。裂尖单元环半径为默认值。取裂纹下端(A点)、上端(C点)、右端(B点)处为定量观点,获取每一扩展步的扩展距离,该阶段裂尖特征点随每一扩展步的变化规律如图14所示。

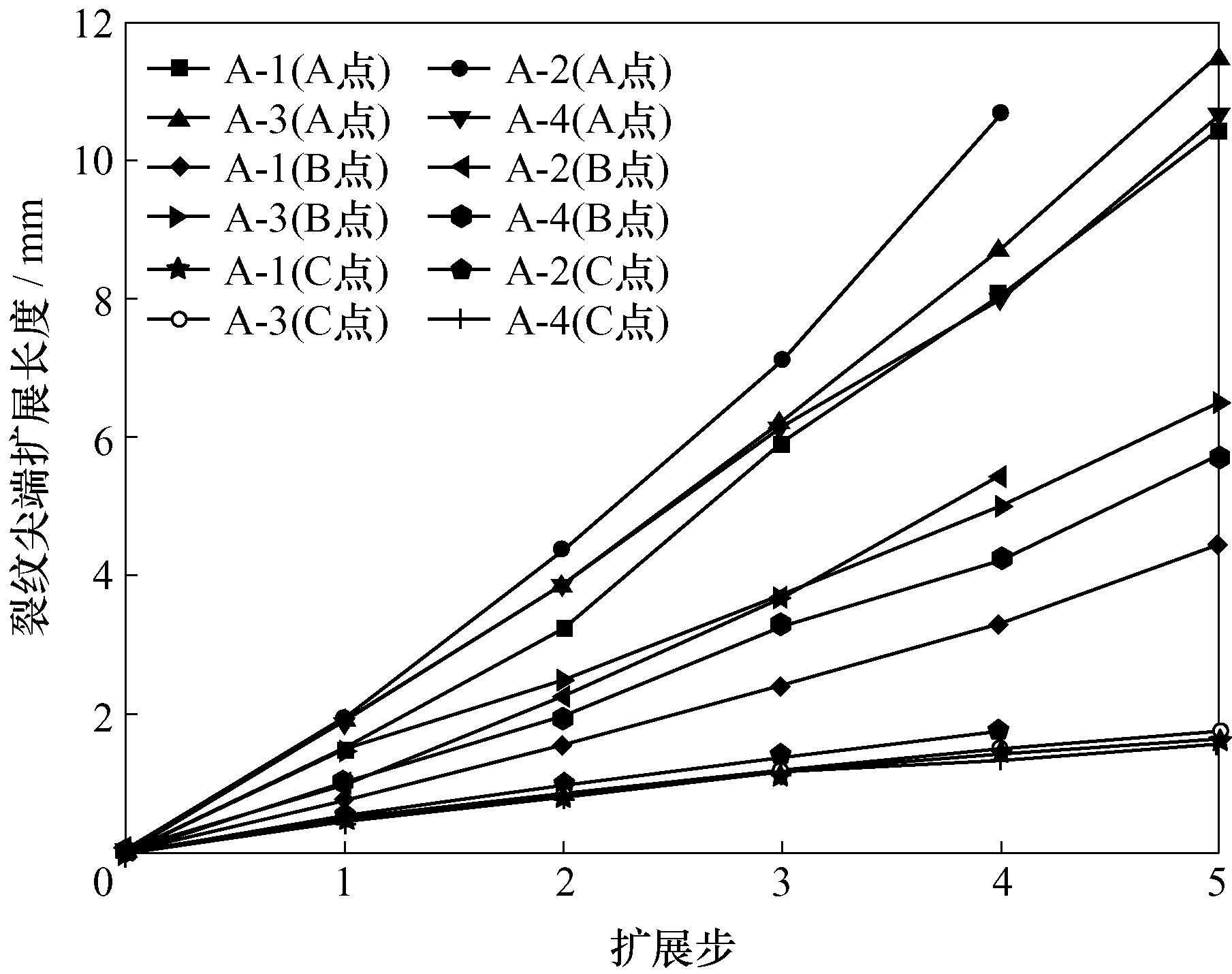
图14扩展步长与扩展前沿示意

由图14可知,裂纹下端(A点)扩展速率最大,裂纹上端(C点)扩展速率最小。且A、C两点的扩展速率有增大的点的扩展速率几乎保持不变。同时可以观察到模型A-2的内裂纹仅用4步就扩展至模型底部,在四组模型中,其裂扩展速度最快。

利用Franc3D软件对三点弯拉下含三维内裂纹模型进行数值模拟,通过对对称加载、非对称加载两组模型开展三维内裂纹扩展规律及断裂特性的研究,得到结论如下:

(1)基于Franc3D软件的数值模拟与室内试验结果具有较好的一致性,该软件是三维裂纹扩展数值模拟的具。

(2)通过裂纹尖端应力强度因子的计算,得出对称加载模型均为Ⅰ型断裂,且裂纹尖端应力强度因子与底部加呈正相关,T应力恒为负值,与带切口SCB试样规律相同。非对称加载模型中出现复合断裂模式,随着右侧加载跨加,K先降低再升高,K/K先变化至0,再逐渐升高。

(3)基于MTS准则对两组试样裂纹扩展与破坏过程进行模拟,对称加载组内裂纹在Ⅰ型断裂模式下进行平面成的贯穿裂纹导致试样断裂成对称的两部分。非对称加载组出现复合断裂模式,裂纹上下尖端出现翼型包裹状后沿着上翼裂纹尖端形成的贯穿裂纹使试样断裂成不对称的两部分。

(4)定量分析对称加载模型裂纹扩展至式样底部的扩展规律,得出裂纹下端扩展速率最大,裂纹上端扩展速且加载跨距与试样半径比为0.6时,裂纹尖端扩展速度最快。

水利水电技术

水利部《水利水电技术》杂志是中国水利水电行业的综合性技术期刊（月刊），为全国中文核心期刊，面向国内外公开发行。本刊以介绍我国水资源的开发、利用、治理、配置、节约和保护，以及水利水电工程的勘测、设计、施工、运行管理和科学研究等方面的技术经验为主，同时也报道国外的先进技术。期刊主要栏目有:水文水资源、水工建筑、工程施工、工程基础、水力学、机电技术、泥沙研究、水环境与水生态、运行管理、试验研究、工程地质、金属结构、水利经济、水利规划、防汛抗旱、建设管理、新能源、城市水利、农村水利、水土保持、水库移民、水利现代化、国际水利等。