在解决旋转相关题型时,同学们尤其要注意题干中是否说明某某三角形为等腰三角形,尤其注意等腰直角三角形、等边三角形、正方形、顶角为特殊角的等腰三角形,遇到以上三角形时,可以考虑利用旋转知识来解题。
以下通过一些实例来帮助同学们理解如何利用等腰三角形的腰转动带动等腰三角形腰所在的三角形转动,从而构造全等三角形利用旋转知识来解决相关问题。
例1:已知在△ACB中,∠ACB=90°,AC=BC,PA=3,PC=2,PB=1,求∠BPC的度数?
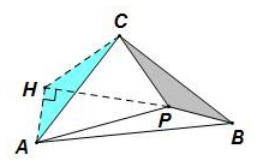
分析:可以判断△ACB为等腰直角三角形,因此可以利用将其中一腰旋转至与另一腰重合,构造全等三角形,来解决问题。
解答过程:
∵在△ACB中,∠ACB=90°,AC=BC,
∴△ACB为等腰直角三角形。
将等腰直角△ACB的一腰BC绕点C顺时针旋转90°与另一腰AC重合,从而带动△CPB顺时针旋转90°至△CHA,
可得△CPB≌△CHA,
∵在△HCP中,CH=CP,∠HCP=90°,
∴△HCP是等腰直角三角形,
∴∠CHP=45°,HP=√2PC=2√2。
在△AHP中,AH=PB=1,AP=3,
∵PH^2+HA^2=(2√2)^2+1^2=9,AP^2=3^2=9
∴PH^2+HA^2=AP^2
∴△AHP是直角三角形,
∴∠PHA=90°,
∴∠BPC=∠AHC=90°+45°=135°。
例题2、如图所示,在等腰Rt△ACB中,∠ACB=90°,D为△ACB外一点,且满足∠ADC=45°,AD=3,CD=4,求BD的长?
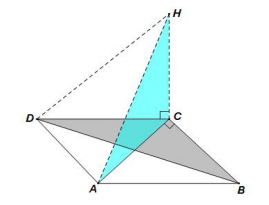
分析:这里已知等腰Rt△ACB,可以将等腰Rt△ACB的一腰BC顺时针旋转90°与另一腰AC重合,从而带动△DCB顺时针旋转90°至△HCA。
解答过程:
将△DCB绕点C顺时针旋转90°至△HCA,则有△DCB≌△HCA,
∴DC=HC,∠DCH=90°,∠HDC=45°,CH=DC=4,
∴在Rt△DCH中,有DH=√2DC=4√2.
又∵∠ADC=45°
∴∠HDA=∠ADC+∠CDH=90°,
在Rt△ADH中,AD=3,DH=4√2,
∴AH=√(AD^2+DH^2)=√(9+32)=√41
∴BD=AH=√41.
例题3、已知如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,且AD=AC。
求证:AB^2+BC^2=BD^2。
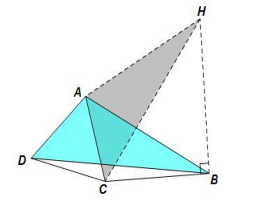
分析:易知△ADC为等边三角形,满足旋转条件。
解答过程:
将△ADB绕点A逆时针旋转60°至△ACH,则可得△ABH为等边三角形,
∵∠ABC=30°
∴∠CBH=∠ABC+∠HBA=90°,
又∵△ADB≌△ACH
∴BD=HC,
∵在直角△CBH中,由勾股定理可得
CH^2=BC^2+BH^2,
又∵在等边△ABH中,AB=BH
∴BD^2=BC^2+AB^2。
例题4、如图,已知在等边△ABC中,点D为△ABC外一点,且满足∠BDC=120°,
试探究BD,DA,DC三者之间满足什么样的数量关系?并说明你的理由。
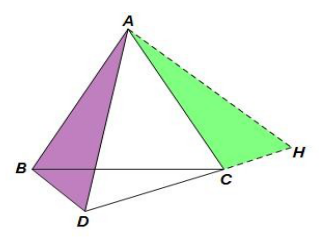
分析:这里△ABC为等边三角形,满足旋转条件。
解答过程:
DA=DB+DC。
理由如下:
将△ABD绕点A逆时针旋转60°至△ACH,
则有△ABD≌△ACH,∠ABD=∠ACH,BD=CH。
∵△ADH为等边三角形
∴DA=DH
在四边形ABDC中,
∵∠BDC=120°,∠BAC=60°,
∴∠ABD+∠ACD=180°,
∴∠ACH+∠ACD=180°,
∴D,C,H三点共线(必须证三点共线,否则扣分)
∵DH=DC+CH,
∴DA=DC+DB。
例题5、如图,已知正方形ABCD,点E为正方形ABCD外一点,AE=2√2,DE=1,求线段CE的最大值?
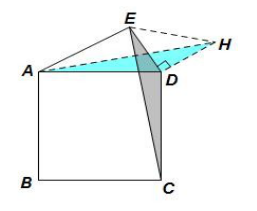
分析:这里出现了正方形ABCD,符合旋转条件。
解答过程:
将△EDC绕点D顺时针旋转90°至△HDA,则有:
△EDC≌△HDA,CE=AH,DE=DH,∠EDH=90°,
∵在等腰直角△EDH中,
∴EH=√2DE=√2。
∴AH≤AE+EH=2√2+√2=3√2,
又∵CE=AH,
∴CE≤3√2。