人民教育出版社八年级数学课本126页有一道数学活动题:
折纸做60度、30度、15度的角。如图:

①将矩形ABCD对折,使AD、BC重合,折痕为EF。
②将AB边折叠,使A点落在EF上,并使折痕BM经过B点,得到线段BN。
观察∠1、∠2、∠3这三个角,可以得到这三个角相等,每个角都是30度。
在探讨这道题的证明过程时我发现:
证法一:∵BE=AB
又∵AB=BN
∴BE=BN
∵△BEN为直角三角形
∴∠3=30°。
∵∠1=∠2
∴∠1=∠2=∠3=30°
证法二:如图二
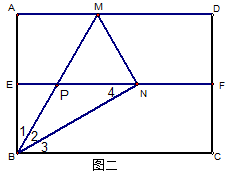
∵EF∥AD,E为AB中点
∴BP=PM
又∵∠BNM=∠A=90°
∴NP=PB=PM
∴∠2=∠4
∵∠4=∠3
∴∠2=∠3
∵∠2=∠1
∴∠1=∠2=∠3=30°。
证法三:如图三,连结AN
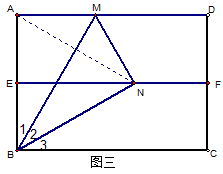
∵EF是矩形ABCD的对称轴
∴NA=NB
又∵BA=BN
∴△ABN是等边三角形
∴∠1=∠2=∠3=30°
三种证法都不一样,但都非常巧妙,在探讨这道几何题的证明过程中,证法二和证法三分别用到了“直角三角形中,一条直角边等于斜边的一半,则这条直角边所对的角是30°”和“三边都相等的三角形是等边三角形”两种方法,由这两种思路继续思考,我们还可以再得出两种折60°的两种方法
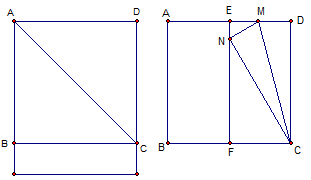
方法一:
①在一张矩形纸片上折出一张最大的正方形ABCD;
②将正方形ABCD沿折痕EF折叠,使AB与CD重合;
③将△CDM沿折痕CM折叠,使D点落在EF上,且使折痕过C点;
④∠BCN=60°。
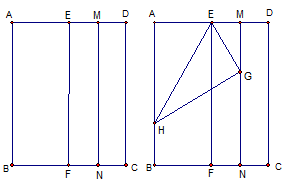
方法二:
①将一张矩形纸片ABCD沿EF对折,使AB与CD重合,再将EFCD沿MN对折,使CD与EF重合;
②将△AEH沿EH折叠,使A点落在MN上,且使折痕过E点;
③∠GEM=60°。
聪明的同学们,你还能想出这道题其他的证法和折法吗?