编辑|花椒

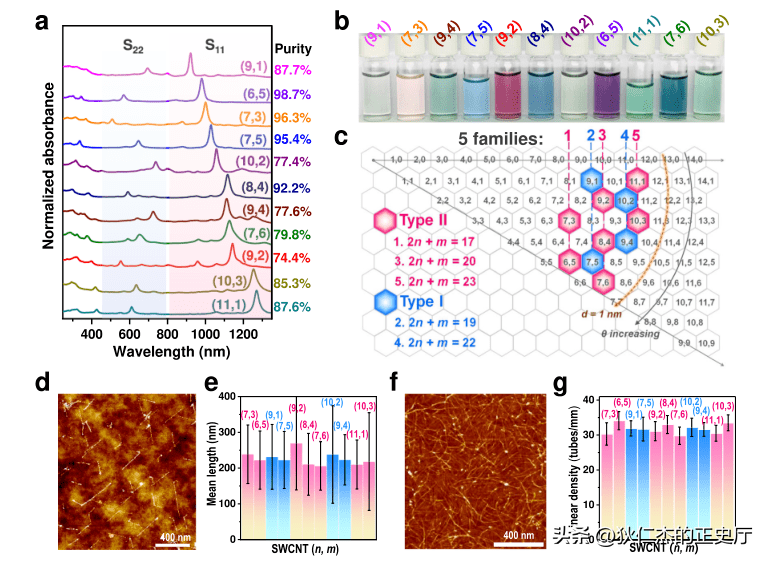
碳纳米管是典型的一维材料,在光电器件中具有潜在的应用价值,实验发现缺陷会使碳纳米管光谱产生红移的卫星峰,但这些红移峰的起源并不清楚。
我们应用多体格林函数理论中的GW方法和Bethe-Salpeter方程,计算了手性的(6,4)碳纳米管的能带和吸收光谱;
在此基础上探讨了空位和Stone-Wales两种本征缺陷对碳纳米管的影响,并与非手性的(n,0)碳纳米管做了比较,揭示了碳纳米管中红移卫星峰的产生机理。

这些发现为碳纳米管在光电子领域的应用提供了一定的参考,具有重要的价值。

低维碳材料(如纳米金刚石、碳纳米管、石墨烯等)具有特殊的结构,在诸多方面表现出不同于常见材料的优异性质,如范霍夫奇点、费米速度重整化、迷你狄拉克点等。
其应用领域十分广泛,具有巨大的商业价值,更有趣的是单壁碳纳米管在光化学和光物理领域表现出独特性质;
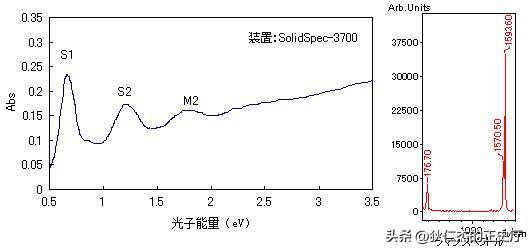
如:单壁碳纳米管的吸收和发射光谱随管径和手性角呈现出“家族式”变化,并可通过其(n,m)指数来表征,半导体碳纳米管中的电子空穴相互作用。
比其他类似带隙的半导体(如晶体硅)中的电子空穴相互作用(结合能)要大一个数量级,这些独特的性质开创了一维碳材料高分辨率传感和高对比度成像应用的新纪元。
实验方面已经进行了大量的工作,以更深入地研究碳纳米管的光化学和光物理过程,并通过引入缺陷来设计具有更多应用的光学器件。
光谱中出现新的红移峰,杂质缺陷也有类似的结果,如氧掺杂、原子氢吸附、外壁功能化等,也会引入红移的卫星峰。
然而,吸附和缺陷也会在碳纳米管的电子能带结构中产生新能级,这些能级可能参与光激发过程。
这些红移卫星峰的解释仍在争论之中,而且由于一维材料独特的电子和光学特性,红移峰的产生原因变得更加复杂。
碳纳米管相关的理论研究工作也已经开展,从微观尺度上利用量子力学方法研究碳纳米管的光电性质是实验研究的重要辅助手段;
从理论上预测其能带结构和光学性质,有助于解决实验上的分歧;碳纳米管的能带结构可以用一个非常简单的模型来描述,该模型被称为区域折叠近似。
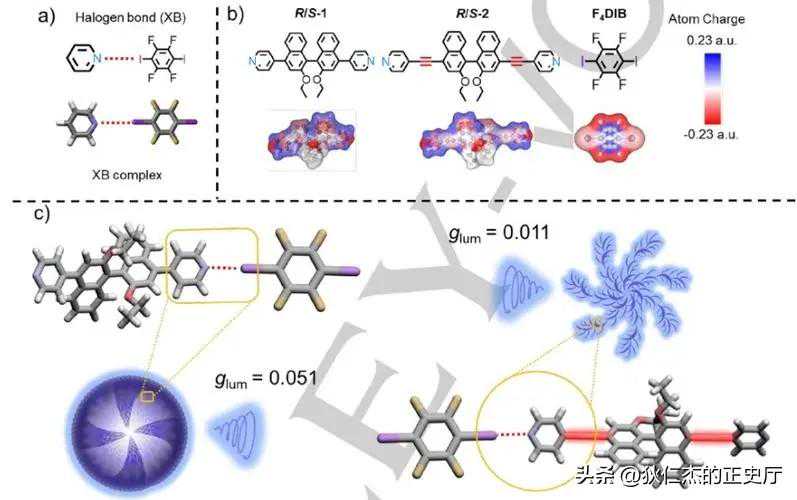
该模型能够适用于大部分碳纳米管,然而部分碳纳米管由于管径太小,会导致相邻电子轨道的重新杂化。
第一性原理计算表明,(5,0)碳纳米管在应该是金属性的;此外,由于曲率的影响,一些金属性的碳纳米管也可能存在非常小的带隙。
缺陷也会对碳纳米管的电子结构产生类似的影响,Choi等人的理论研究证明缺陷诱导态与缺陷排列密切相关。
虽然碳纳米管电子结构的研究已经很多,但其光化学和光物理过程的理论研究还很少。
用氢饱和的分子模型讨论了取代基对碳纳米管光谱的影响,然而碳纳米管的周期性要求其从第一性原理进行计算。
多体格林函数理论是研究物质激发态性质的第一性原理方法,可通过GW近似和Bethe-Sal-peter方程研究周期性体系的电学和光学性质。
在之前的工作中,我们研究了一系列非手性的(n,0)管,并解释了其光谱变化规律,以及本征和杂质缺陷对光谱的影响。
然而实验上更多采用手性碳纳米管,其晶胞相对非手性碳纳米管更加复杂,我们将以(6,4)碳纳米管为例;

研究手性碳纳米管的光谱,并探讨不同缺陷的影响,提出手性碳纳米管中红移卫星峰的产生机理。
理论与计算方法我们采用了手性的(6,4)碳纳米管作为模型进行研究,无缺陷的(6,4)管原胞含有152个碳原子;引入的缺陷包括空位和Stone-Wales缺陷。
所有的结构优化均采用了Perdew-Burke-Ernzerhof泛函、Troullier-Martins规范-守恒赝势和双基组,并在SIESTA程序中完成。
由于碳纳米管的一维周期性,计算过程中采用了周期性边界条件,并保证碳纳米管的管间距大于10括。
K点和截断能都经过严格的测试,保证结果的准确性,构型优化结构,其中蓝色部分表示缺陷所在范围。
(n,0)碳纳米管的导带底和夹带顶均位于点,而(6,4)管的导带底和价带顶略有偏移,这种偏移可通过区域折叠近似进行解释。
DFT和GW计算的(6,4)碳纳米管带隙分别为1.07eV和2.20eV,准粒子结果对DFT计算结果的校正(剪刀位移)为1.03eV;
碳纳米管的剪刀位移相对于三维周期性体系(如晶体硅)要大很多,可以认为是由于其独特的准一维库伦效应引起的。
黑色曲线显示了Bethe-Salpeter方程计算的(6,4)碳纳米管的光学吸收谱。
由于碳纳米管的“去极化效应”,即当入射光与管轴方向平行时,光的电场的方向垂直于管轴方向,因此不会有明显吸收峰出现。
当入射光方向垂直于管轴时,“去极化效应”基本可以忽略,因此在我们的计算过程中,将光的电场方向设置为与碳纳米管的轴向相同。
峰A和峰B分别代表碳纳米管的第一吸收峰和第二吸收峰,即由范霍夫奇异性引起的前两个亮态:E11和E22,而其他跃迁则是光学禁阻的暗态。
这两个激发态的能量分别为1.41eV和2.05eV,与实验的结果符合非常好。
该激发态的电子和空穴分布如图2(c)所示,其分布范围要大于计算所用的碳纳米管原胞,具有一定的非局域特性。
与完美碳纳米管的能带相比,其能级结构更为复杂,空位缺陷使得碳纳米管能带发生了分裂,并出现了一条近乎水平的能带。
轨道分布表明该能带在点对应的电子态主要分布在空位缺陷周围的原子上,属于局域缺陷态。
由于能带分裂和局域缺陷态的存在,空位缺陷碳纳米管的带隙显著降低,从2.20eV降到1.50eV。
Stone-Wales缺陷碳纳米管的能带也表现出类似的能级分裂和局域缺陷态,其带隙为2.0eV.这些变化是起源于碳纳米管几何构型的变化;
当缺陷存在时,晶胞中所有原子都会弛豫,并引起对称性的变化,最后导致碳纳米管的能带变化。
在准粒子能带的基础上,我们计算了缺陷存在时碳纳米管的吸收光谱,与完美碳纳米管的光谱相比吸收峰产生了明显变化,出现了很多红移的卫星峰。
这些变化可归因于缺陷引起的碳纳米管电子结构的变化,如能级发生分裂、新的局域缺陷态生成。
光谱跃迁选律也因此发生变化,一些暗的激发态变亮,光谱中出现红移卫星峰,而由范霍夫奇异性引起的前两个亮态减弱,吸收峰强度降低。

在空位缺陷存在时,最低的吸收峰A能量为0.80eV,该吸收峰的跃迁是由价带顶向局域缺陷态的跃迁。
其中红色部分表示电子的分布,蓝色部分表示空穴的分布,可以看出,电子的分布是局域的,与能带的分析结果一致。
Stone-Wales缺陷碳纳米管光谱的也发生了类似的变化,其最低吸收峰的能量为1.25等人的实验表明,(6,4)碳纳米管的缺陷红移吸收峰比完美碳纳米管的最低吸收峰低约0.11-0.19eV。
我们的计算结果为0.16eV,与实验一致在之前工作中,我们研究了氧掺杂的碳纳米管的光学性质并指出掺杂引起能带的分裂,进而改变光谱。

本文采用多体格林函数理论精确计算了手性的(6,4)碳纳米管的能带和吸收光谱,并研究了空位缺陷和Stone-Wales缺陷对其影响。

与非手性的半导体型(n,0)碳纳米管比较,多体格林函数理论计算的手性碳纳米管的带隙拉伸基本一致,但对称性降低,其能带的简并度也相应降低;
且能带的价带顶和导带底不再位于布里渊区中心的点处;光谱性质方面,手性(6,4)碳纳米管与非手性(n,0)管的光谱跃迁旋律一样。
吸收光谱中出现两个明显的吸收峰,吸收峰对应的激子的电子空穴相互作用能和激子分布也基本一致,但激子的跃迁位置不同。
当引入缺陷后,能带中出现局域的缺陷态,这些缺陷态会改变碳纳米管的跃迁选律,进而出现红移的吸收峰。
这些计算的结果与实验结果相吻合,解释了实验中缺陷碳纳米管红移卫星峰的产生机理,并可望利用这种拓扑缺陷扩展碳纳米管在光电器件的应用。
参考文献:
[1]包镍碳纳米管提高烧结银的断裂韧性[J].代岩伟;昝智;秦飞.电子与封装,2022(11)
[2]飞秒激光诱导多壁碳纳米管与金属电极连接的实验研究[J].梅欢欢;崔健磊;程杨;何小桥;梅雪松.中国激光,2021(08)
[3]碳纳米管提升氧化亚硅负极稳定性的起源(英文)[J].周军华;王佳琪;施启涛;连雪玉;刘玉;刘立军;AlicjaBachmatiuk;孙靖宇;杨瑞枝;Jin-HoChoi;ü
[4]超长碳纳米管实现超高产率制备[J]..浙江化工,2023(01)
[5]碳纳米管改性氟橡胶的性能研究[J].李越;程文佳;刘明泰;尤黎明;徐凤祥;李光大;史学涛.中国塑料,2023(03)
[6]苏州纳米所单手性碳纳米管高纯度分离技术研究获进展[J]..食品与生物技术学报,2021(12)
[7]表面活性剂分散多壁碳纳米管机理及性能评价[J].陈泽宇;刘静;蒲春生;李旭;白云.精细化工,2022(02)
[8]碳纳米管间碘链负载量和分布的导热强化探究[J].邹瀚影;冯妍卉;邱琳;张欣欣.工程热物理学报,2022(03)
[9]碳纳米管材料在服装行业的应用[J].何晓霞;宋向荣;宋慎群;黄惠标.化纤与纺织技术,2022(01)
[10]单根碳纳米管的“基因”编辑[J].张锦.科学通报,2022(14)